Computers work through a complex interaction of hardware and software components that enable them to process, store, and communicate information.
When data is inputted to the computer, the computer then process the data using its CPU. It then uses its memory as a temporary storage, and the physical storage to store data for longer periods of time. The computer then outputs the data it processed.
The number 2,147,483,647 is closely related to the way computers handle integers.
In the context of computing, the value of 2,147,483,647 is significant because it represents the highest positive value that can be represented using a 32-bit system.
This value is derived from the binary representation of a 32-bit signed integer, where the most significant bit is reserved for representing the sign of the number, leaving 31 bits for the actual value.
This value arises due to the way computer memory is allocated and how data types are represented in binary form.
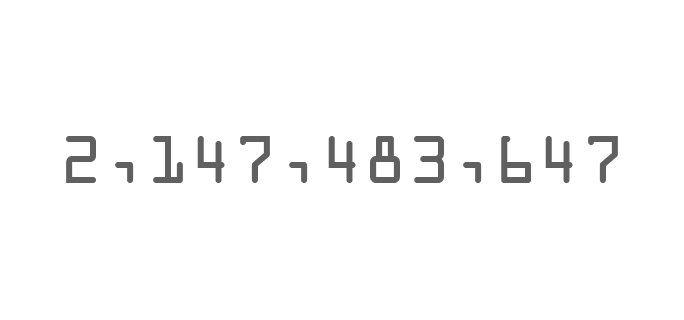
It was Leonhard Euler who found that 2,147,483,647 is a Mersenne prime, a prime number that is one less than a power of two.
The number 2,147,483,647 is known as the eighth Mersenne prime, equal to 231 − 1. It's also one of only four known double Mersenne primes.
But in computing, the number 2,147,483,647 can be referred to as a "magic number," because it defines the upper limit of what can be stored in a 32-bit system, a design that has been used since the earliest days of electronic computing.
This is because 32-bit system can store 232 different values, meaning that it can store 4,294,967,295 (232 − 1) for representation as an (unsigned) binary number, and −2,147,483,648 (−231) through 2,147,483,647 (231 − 1) for representation as two's complement.
Not only that the value is the largest largest positive or negative number that can be stored in a single 32-bit variable, it's also the limit of many common data types and algorithms.
For example, in the C programming language, the int data type is typically 32 bits wide, so the largest value that can be stored in an int variable is 2,147,483,647. Similarly, many common algorithms, such as sorting and searching algorithms, are designed to work with 32-bit integers.
This number has a special significance for C programmers, who know it by the name INT_MAX, and for C++ programmers, who demystify the digits as std::numeric_limits. It is also the largest signed value you can fit in a 32-bit register.
Besides that, 2,147,483,647 is also the maximum number of rows in a MySQL table , the maximum number of vertices in a graph that can be represented by a 32-bit variable.
In essence, the number 2,147,483,647 is the threshold of computing, considered the largest number that can be represented by a 32-bit computer.
When the CPU processes data and instructions, it can only handle numbers within the range of the data type it's designed for.
Exceeding this 2,147,483,647 value will lead to an overflow, where the number might wrap around to the lowest possible negative value or cause errors in the program.
Because of the limitations of 32-bit systems, the use of this number as a limit or boundary is quite common in software development.
Understanding this limitation is crucial for programmers and software developers to ensure that their programs can handle values within this range appropriately.

Sometimes, and chances are, there are ways to break through this limit.
Examples include older games, including older mobile games.
From Tetris, and all the way to Subway Surfer, for example.
Players who managed to reach the 2,147,483,647 score, would see the game start glitching.
It's worth noting that in games, the number 2,147,483,647 often becomes a hard limit for various statistics in video games, such as points or money, but only if they are represented by signed 32-bit integers, and not using floating-point, double-precision or arbitrary-precision.
Other examples, include Old School RuneScape and Grand Theft Auto V, where the 2,147,483,647 is used as the maximum amount of coins (or any other item) that a player can hold at once with normal methods, known as a "max cash stack".
It's also worth noting that where an unsigned instead of signed 32-bit integer is used, the 2,147,483,647 limit might be extended to 4,294,967,295.

Fortunately, the advancements of technology allows the development of 64-bit systems.
With it, this limitation has been significantly mitigated, allowing for much larger numbers to be represented without the risk of overflow.
In 64-bit systems, that the limit of computing has increased to a theoretical limit of 18,446,744,073,709,551,616 bytes, or 18 quintillion.
The maximum amount of memory that can be addressed by a 64-bit processor is a significant improvement to 2,147,483,647 on 32-bit systems.
Therefore, the correlation with 2,147,483,647 underscores the significance of data representation and the constraints of older computing architectures.
Because the limitations are significantly mitigated, software can process and work on much larger numbers, and that much higher values can be presented without the risk of overflow.
This results in larger memory addressing, allowing more complex computations, and the handling of extensive datasets and applications that demand high computational capabilities.
