
Since the invention of computers, humans have dreamed of a world where technology can pave the clearer and easier future.
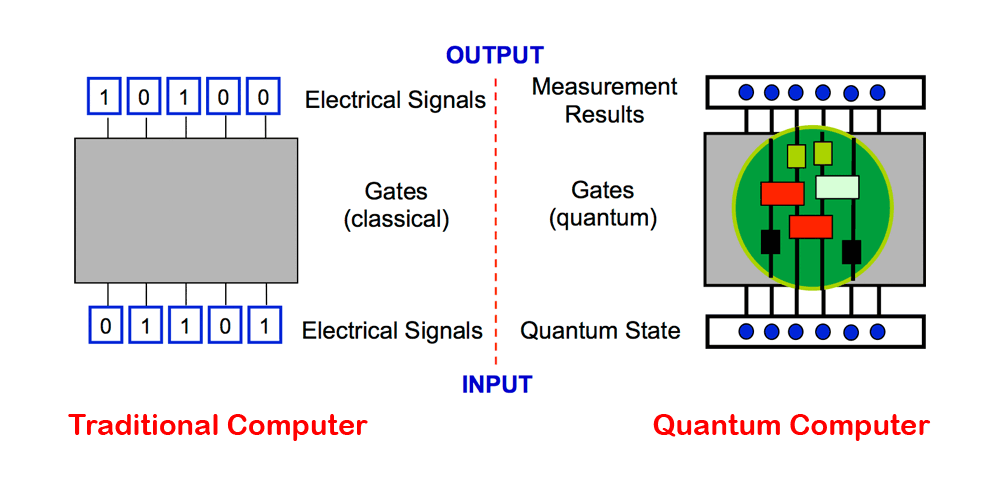
Traditional computers that work in "bits" have powered everything from a PC, laptop, to a smartphone and even a supercomputer on research facilities. For most people, catching up to the fast pace technology is already too much. But to some, no, traditional computers are simply not enough.
This is where we advanced to the next step of computing: quantum computers.
These computers work in "qubits". Oppose to "bits" that can only have either 1 or 0 state, "qubits" can have a superposition of both states at the same time. This property is fundamental to quantum computing, and this is something that in theory, makes quantum computers far superior than traditional computers, no matter how capable they are.
But first, we have to have an evidence to prove that. Computer scientists searched for this using specific kind of computational problem since 1993. That year was also when Dan Simon invented an oracle problem for which a quantum computer would be exponentially faster than a conventional computer.
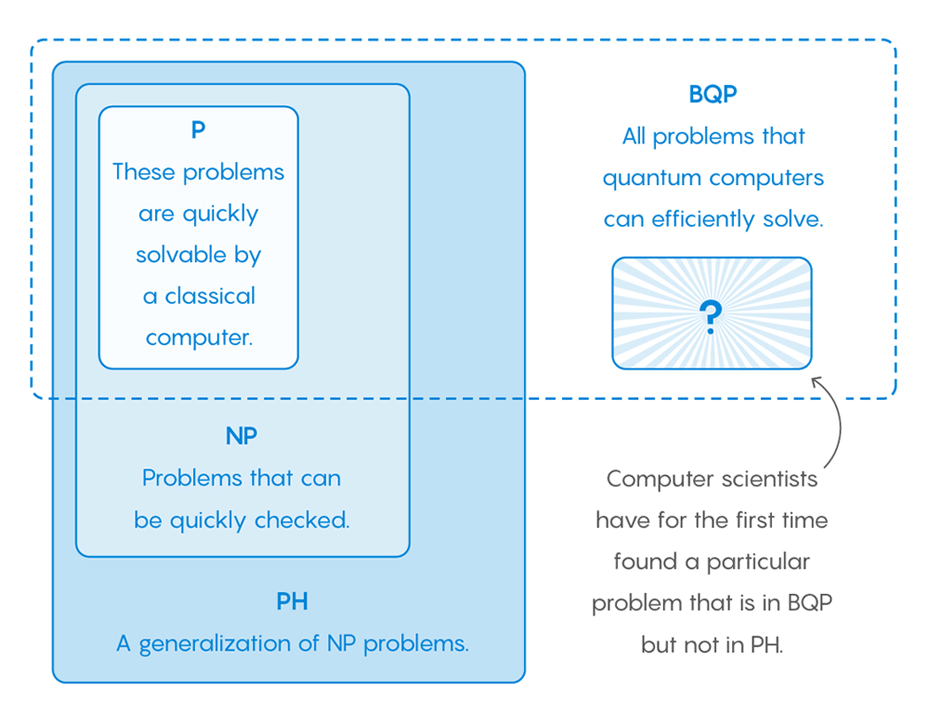
Computer scientists Ethan Bernstein and Umesh Vazirani defined a new complexity class that they called BQP, or "bounded-error quantum polynomial time," which encompasses all problems that quantum computers can solve.
Since then, computer scientists have tried to contrast BQP with a class of problems known as "PH," or "polynomial hierarchy", which encompasses all the problems workable by any possible classical computer.
But all the attempts ended with no result.
That until 2018 when computer scientists Ran Raz and Avishay Tal provide strong evidence that quantum computers indeed possess a computing capacity beyond anything traditional computers could ever achieve.
Raz, a professor at Princeton University and the Weizmann Institute of Science, and Tal, a postdoctoral fellow at Stanford University, defined a specific kind of computational problem. They prove that quantum computers do have the ability to solve certain problems efficiently, while traditional computers would struggle or bog down forever trying to solve it.
In their paper, the result does not elevate quantum computers over traditional computers in any practical sense, as theoretically, computer scientists already knew that quantum computers should be better than traditional computers.
What Raz and Tal demonstrate is that, quantum computers are really a different machine, something that is category apart from traditional computers. Even when traditional computers succeed in computation beyond anything imaginable at a given time, quantum computers should be able to stand beyond them.
This was proven with an algorithms, let's say, for testing whether a number is a prime number. The two most famous complexity classes here are "P" and "NP."
P is where all the problems that a traditional computer can solve quickly (example: is this a prime number?"), and NP is where all the problems that traditional computers can’t necessarily solve quickly (example: what are this number's prime factors?). Where PH stands here, is as the generalization of NP.
The scientists could not determine whether BQP contains problems not found in PH. This was difficult because in definition, the scientists need to identify something that traditional computers could not verify the answer.
On their paper, Raz and Tal mentions oracle which separates BQP and PH. The actual way to distinguish between the two complexity classes, is to measure the computational time required to solve a problem in each computer.
Since the computer scientists don’t have a very sophisticated understanding of, or ability to measure, actual computation time, they measure something else that they hope will provide insight into the computation times they can’t measure.
This is by working out the number of times a computer needs to consult an oracle for an answer. The more a computer asks the oracle for hint, the slower it gets. And here, Raz and Tal succeeded in using oracle separation to distinguish BQP from PH.
Raz and Tal prove that a quantum computer needs far fewer hints than a traditional computer to solve the Forrelation problem. This is where the computers need to decide whether one Boolean function is highly correlated with the Fourier transform of a second function.
In a paper in 2014, Scott Aaronson, Andris Ambainis concluded that Forrelation is a problem that optimally separates quantum from traditional computing.
Quantum computer needed only one hint. While in PH, even with with unlimited hints, there’s no available algorithm that can solve the problem.
"This means there is a very efficient quantum algorithm that solves that problem," said Raz. "But if you only consider classical algorithms, even if you go to very high classes of classical algorithms, they cannot."
Raz and Tal had actually nearly achieved this result, which was also in 2014. But they couldn’t complete one of the final step. In 2018, Tal heard a talk on a paper on pseudorandom number generators and found the techniques in that paper were just the ones that he and Raz needed to finish their own.
"This was the missing piece,” said Tal.
